সংখ্যা বিশ্লেষণ হলো গণিতের একটি শাখা যা পূর্ণসংখ্যা, তাদের বৈশিষ্ট্য এবং সম্পর্ক নিয়ে কাজ করে। গুণিতক হলো সংখ্যা বিশ্লেষণের একটি মৌলিক ধারণা যা দুই বা ততোধিক সংখ্যার মধ্যে সম্পর্ক বর্ণনা করে। এই পোস্টে, আমরা গুণিতকের ধারণা, বিভিন্ন ধরণের গুণিতক, এবং কিছু গুরুত্বপূর্ণ প্রয়োগ নিয়ে আলোচনা করব।

Table of contents
গুণিতক (Multiple) কাকে বলে?
গুণিতকের সংজ্ঞা: দুটি বা ততোধিক সংখ্যার মধ্যে সম্পর্ককে গুণিতক বলে যা বোঝায় যে একটি সংখ্যা (গুণফল) অন্য সংখ্যা (গুণিতক) দ্বারা সম্পূর্ণ ভাগ করা যায়। উদাহরণস্বরূপঃ 3, 6, 9, 12, 15, 18, 24, 36 ইত্যাদি হল 3-এর গুণিতক।
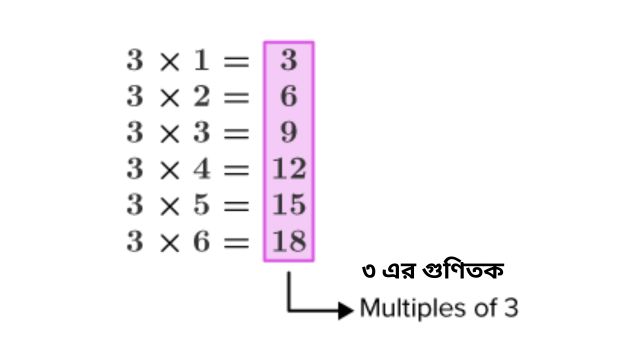
সহজ কথায়, ধরা যাক, a হলো একটি সংখ্যা এবং b হলো একটি গুণিতক। তাহলে,
- a কে b দ্বারা ভাগ করলে কোনো ভাগশেষ থাকবে না।
- অর্থাৎ, a = b × n, যেখানে n হলো একটি পূর্ণসংখ্যা।
উদাহরণ:
- 6 হলো 12 এর একটি গুণিতক কারণ 12 ÷ 6 = 2 (এবং ভাগশেষ 0)।
- 15 হলো 30 এর একটি গুণিতক কারণ 30 ÷ 15 = 2 (এবং ভাগশেষ 0)।
গুণিতক এর ধারণা
গুণিতক হলো এমন একটি সংখ্যা যা দ্বারা অন্য একটি সংখ্যাকে ভাগ করলে কোনো ভাগশেষ থাকে না। সহজ কথায়, ধরা যাক, a হলো একটি সংখ্যা এবং b হলো একটি গুণিতক।
তাহলে,
- a কে b দ্বারা ভাগ করলে কোনো ভাগশেষ থাকবে না।
- অর্থাৎ, a = b × n, যেখানে n হলো একটি পূর্ণসংখ্যা।
উদাহরণ:
- 6 হলো 12 এর একটি গুণিতক কারণ 12 ÷ 6 = 2 (এবং ভাগশেষ 0)।
- 15 হলো 30 এর একটি গুণিতক কারণ 30 ÷ 15 = 2 (এবং ভাগশেষ 0)।
গুণিতকের কিছু গুরুত্বপূর্ণ বৈশিষ্ট্য
- প্রতিটি সংখ্যার নিজেই একটি গুণিতক।
- 0 (শূন্য) এর কোনো গুণিতক নেই।
- একটি সংখ্যার সকল গুণিতক অসীম সংখ্যক।
- দুটি সংখ্যার লঘিষ্ঠ সাধারণ গুণিতক হলো ঐ দুটি সংখ্যার সকল সাধারণ গুণিতকের মধ্যে সবচেয়ে ছোট সংখ্যা।
- একটি সংখ্যার বর্গ গুণিতক এবং ঘন গুণিতকও ঐ সংখ্যার সাধারণ গুণিতক।
গুণিতকের প্রকারভেদ
গুণিতক হলো এমন একটি সংখ্যা যা দ্বারা অন্য একটি সংখ্যাকে ভাগ করলে কোন ভাগশেষ থাকে না। গুণিতকগুলোকে বিভিন্নভাবে শ্রেণীবদ্ধ করা যায়।
1. সাধারণ গুণিতক (Common Multiple):
দুটি বা ততোধিক সংখ্যার সাধারণ গুণিতক হলো এমন একটি সংখ্যা যা ঐ সকল (দুই বা ততোধিক) সংখ্যাকে ভাগ করে।
সহজ কথায়, ধরা যাক, a এবং b হলো দুটি সংখ্যা। তাহলে, a এবং b এর সাধারণ গুণিতক হলো এমন একটি সংখ্যা c যা:
- a কেও ভাগ করে
- b কেও ভাগ করে
উদাহরণ:
- 2 এবং 3 এর সাধারণ গুণিতক হলো 6, 12, 18, ইত্যাদি।
- 6 এবং 12 এর সাধারণ গুণিতক হলো 6, 12, 18, 24, 36, ইত্যাদি।
- 15 এবং 20 এর সাধারণ গুণিতক হলো 60, 120, 180, ইত্যাদি।
সাধারণ গুণিতক নির্ণয়ের বিভিন্ন পদ্ধতি:
1. তালিকা পদ্ধতি:
- a এবং b এর সকল গুণিতকের একটি তালিকা তৈরি করুন।
- দুটি তালিকা তুলনা করে সাধারণ গুণিতক খুঁজে বের করুন।
উদাহরণ:
6 এবং 12 এর সাধারণ গুণিতক নির্ণয়:
6 এর গুণিতক: 6, 12, 18, 24, 30, 36, 42, 48, 54, 60, …12 এর গুণিতক: 12, 24, 36, 48, 60, 72, 84, 96, 108, 120, …
সাধারণ গুণিতক: 6, 12, 18, 24, 36, 48, 60, …
2. লঘিষ্ঠ সাধারণ গুণিতক (Least Common Multiple):
দুটি বা ততোধিক সংখ্যার লঘিষ্ঠ সাধারণ গুণিতক হলো ঐ সকল সংখ্যাকে ভাগ করার জন্য সবচেয়ে ছোট সংখ্যা। অর্থাৎ, লঘিষ্ঠ সাধারণ গুণিতক (ল.সা.গু.) হলো দুটি বা ততোধিক সংখ্যার সবচেয়ে ছোট সাধারণ গুণিতক।
সহজ কথায়, ধরা যাক, a এবং b হলো দুটি সংখ্যা। তাহলে, a এবং b এর ল.সা.গু. হলো, যেকোন একটি সংখ্যা c যা:
- a কেও ভাগ করে
- b কেও ভাগ করে
- c এর চেয়ে ছোট কোন সংখ্যা a এবং b কে ভাগ করে না
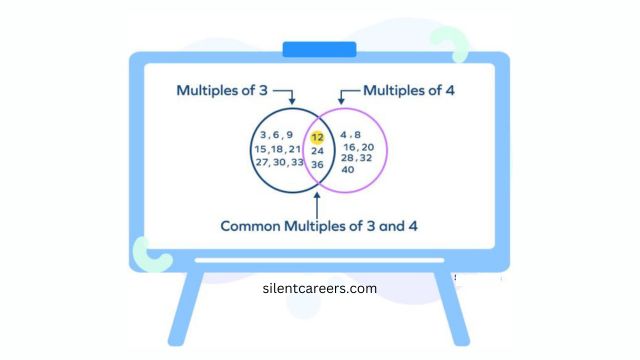
উপরের ছবিতে দেখুন, ৩ ও ৪ এর সাধারন (Common) গুণিতক হল ১২,২৪ এবং ৩৬। এই কমনগুলোর মধ্যে আবার সবচেয়র ছোট গুণিতক হল ১২। তাই ১২ কে ৩ ও ৪ লঘিষ্ট সাধারণ গুণিতক বলা হয়।
উদাহরণ:
- 2 এবং 3 এর লঘিষ্ঠ সাধারণ গুণিতক হলো 6।
- 6 এবং 12 এর ল.সা.গু. হলো 12।
- 15 এবং 20 এর ল.সা.গু. হলো 60।
ল.সা.গু. নির্ণয়ের বিভিন্ন পদ্ধতি:
1. তালিকা পদ্ধতি:
- a এবং b এর সকল গুণিতকের একটি তালিকা তৈরি করুন।
- দুটি তালিকা তুলনা করে সবচেয়ে ছোট সাধারণ গুণিতক খুঁজে বের করুন।
উদাহরণ:
6 এবং 12 এর ল.সা.গু. নির্ণয়:
6 এর গুণিতক: 6, 12, 18, 24, 30, 36, 42, 48, 54, 60, …
12 এর গুণিতক: 12, 24, 36, 48, 60, 72, 84, 96, 108, 120, …
সুতরাং, ল.সা.গু. = 12
3. অভাজ্য গুণিতক (Prime Multiple):
একটি সংখ্যার অভাজ্য গুণিতক হলো ঐ সংখ্যাকে ভাগ করার জন্য একটি অভাজ্য সংখ্যা।
উদাহরণ: 12 এর অভাজ্য গুণিতক হলো 2, 3, 4, 6, 12।
4. বর্গ গুণিতক (Square Multiple):
একটি সংখ্যার বর্গ গুণিতক হলো ঐ সংখ্যাকে ভাগ করার জন্য একটি বর্গ সংখ্যা।
উদাহরণ: 16 এর বর্গ গুণিতক হলো 16, 64, 256, ইত্যাদি।
5. ঘন গুণিতক (Cube Multiple):
একটি সংখ্যার ঘন গুণিতক হলো ঐ সংখ্যাকে ভাগ করার জন্য একটি ঘন সংখ্যা।
উদাহরণ: 8 এর ঘন গুণিতক হলো 8, 64, 512, ইত্যাদি।
গুণিতকের ব্যবহার
- লঘিষ্ঠ সাধারণ গুণিতক দুটি বা ততোধিক সংখ্যার তুলনা করার জন্য ব্যবহৃত হয়।
- সাধারণ গুণিতক ব্যবহার করে দুটি বা ততোধিক সংখ্যার সমন্বয় নির্ধারণ করা হয়।
-
গুণিতক ব্যবহার করে বিভিন্ন সমস্যার সমাধান করা হয়, যেমন:
- সর্বনিম্ন সংখ্যা নির্ণয় করা যা দুটি বা ততোধিক সংখ্যাকে ভাগ করে।
- দুটি বা ততোধিক সংখ্যার সমন্বয় নির্ধারণ করা।
- একটি নির্দিষ্ট সংখ্যা দ্বারা কতগুলো সংখ্যা ভাগ করা যায় তা নির্ণয় করা।
