আজকের আর্টিকেলে আমরা বৃত্ত কাকে বলে?, বৃত্তের পরিধি, ক্ষেত্রফল ও ব্যাসার্ধ নির্ণয়ের সূত্র – চিত্রসহ উদাহরণ ইত্যাদি সম্পর্কে আলোচনা করব।
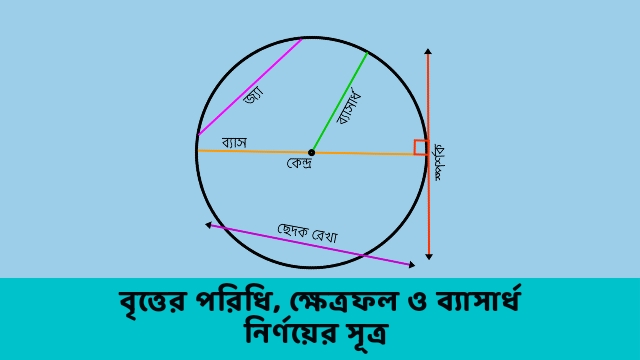
Table of contents
বৃত্ত কাকে বলে? বৃত্ত কি?
বৃত্ত হলো একটি সমতল আকৃতি যা নিম্নলিখিত বৈশিষ্ট্যগুলি দ্বারা সংজ্ঞায়িত করা হয়:
- কেন্দ্র: বৃত্তের একটি নির্দিষ্ট বিন্দু যা সমস্ত বিন্দু থেকে সমান দূরত্বে অবস্থিত।
- বিন্দু: কেন্দ্র থেকে সমান দূরত্বে অবস্থিত বৃত্তের যেকোনো বিন্দু।
- ব্যাসার্ধ: কেন্দ্র থেকে যেকোনো বিন্দুর দূরত্ব।
- ব্যাস: বৃত্তের মধ্য দিয়ে অতিক্রম করে কেন্দ্রের মধ্য দিয়ে যাওয়া দীর্ঘতম রেখা, যার দৈর্ঘ্য ব্যাসার্ধের দ্বিগুণ।
- পরিধি: বৃত্তের রেখাচিত্রের মোট দৈর্ঘ্য।
- ক্ষেত্রফল: বৃত্তের ভেতরের এলাকা।
উদাহরণ:
- একটি প্লেট
- একটি চাকা
- একটি পয়সা
- একটি থালা
বৃত্তের বৈশিষ্ট্য:
- বৃত্তের যেকোনো দুটি ব্যাস সমান্তরাল।
- বৃত্তের যেকোনো দুটি ব্যাসার্ধ সমান।
- বৃত্তের পরিধি 360 ডিগ্রি।
- বৃত্তের ক্ষেত্রফল πr²।
উদাহরণসহ বৃত্তের ক্ষেত্রফল নির্ণয়ের সূত্র
বৃত্তের ক্ষেত্রফল নির্ণয়ের সূত্র হলো: πr²
যেখানে:
- π (পাই) একটি ধ্রুবক যার মান প্রায় 3.1416।
- r হল বৃত্তের ব্যাসার্ধ, যা বৃত্তের কেন্দ্র থেকে যেকোনো বিন্দুতে বৃত্তের পরিধির দৈর্ঘ্যের অর্ধেক।
উদাহরণস্বরূপ:
ধরা যাক একটি বৃত্তের ব্যাসার্ধ 5 সেন্টিমিটার।
এই বৃত্তের ক্ষেত্রফল নির্ণয় করতে, আমরা নিম্নলিখিত সূত্রটি ব্যবহার করব:
πr² = 3.1416 * 5 cm * 5 cm
= 78.54 cm²
অর্থাৎ, এই বৃত্তের ক্ষেত্রফল প্রায় 78.54 বর্গ সেন্টিমিটার।
বৃত্তের ক্ষেত্রফল নির্ণয়ের জন্য কিছু টিপস:
- ব্যাসার্ধ সঠিকভাবে পরিমাপ করুন: বৃত্তের ক্ষেত্রফল নির্ণয়ের জন্য সবচেয়ে গুরুত্বপূর্ণ বিষয় হল ব্যাসার্ধ সঠিকভাবে পরিমাপ করা। আপনি একটি রুলার, টেপ পরিমাপকারী বা কম্পাস ব্যবহার করতে পারেন।
- π এর মান মনে রাখবেন: π এর মান 3.1416 প্রায়। আপনি একটি ক্যালকুলেটর ব্যবহার করতে পারেন বা π এর মান মনে রাখার জন্য একটি স্মৃতিশক্তি সহায়ক ব্যবহার করতে পারেন।
- সঠিক একক ব্যবহার করুন: বৃত্তের ক্ষেত্রফলের একক ব্যাসার্ধের এককের সাথে সামঞ্জস্যপূর্ণ হতে হবে। যদি ব্যাসার্ধ সেন্টিমিটারে পরিমাপ করা হয়, তাহলে ক্ষেত্রফল বর্গ সেন্টিমিটারে হবে।
বৃত্তের পরিধি নির্ণয়ের সূত্র
বৃত্তের পরিধি নির্ণয়ের সূত্র হলো: 2πr
যেখানে:
- π (পাই) একটি ধ্রুবক যার মান প্রায় 3.1416।
- r হল বৃত্তের ব্যাসার্ধ, যা বৃত্তের কেন্দ্র থেকে যেকোনো বিন্দুতে বৃত্তের পরিধির দৈর্ঘ্যের অর্ধেক।
উদাহরণস্বরূপ:
ধরা যাক একটি বৃত্তের ব্যাসার্ধ 5 সেন্টিমিটার।
এই বৃত্তের পরিধি নির্ণয় করতে, আমরা নিম্নলিখিত সূত্রটি ব্যবহার করব:
2πr = 2 * 3.1416 * 5 cm
= 31.42 cm
অর্থাৎ, এই বৃত্তের পরিধি প্রায় 31.42 সেন্টিমিটার।
বৃত্তের পরিধি নির্ণয়ের জন্য কিছু টিপস:
- ব্যাসার্ধ সঠিকভাবে পরিমাপ করুন: বৃত্তের পরিধি নির্ণয়ের জন্য সবচেয়ে গুরুত্বপূর্ণ বিষয় হল ব্যাসার্ধ সঠিকভাবে পরিমাপ করা। আপনি একটি রুলার, টেপ পরিমাপকারী বা কম্পাস ব্যবহার করতে পারেন।
- π এর মান মনে রাখবেন: π এর মান 3.1416 প্রায়। আপনি একটি ক্যালকুলেটর ব্যবহার করতে পারেন বা π এর মান মনে রাখার জন্য একটি স্মৃতিশক্তি সহায়ক ব্যবহার করতে পারেন।
- সঠিক একক ব্যবহার করুন: বৃত্তের পরিধির একক ব্যাসার্ধের এককের সাথে সামঞ্জস্যপূর্ণ হতে হবে। যদি ব্যাসার্ধ সেন্টিমিটারে পরিমাপ করা হয়, তাহলে পরিধি সেন্টিমিটারে হবে।
বৃত্তের পরিধি এবং ক্ষেত্রফলের মধ্যে পার্থক্য
- পরিধি: বৃত্তের পরিধি হল বৃত্তের রেখাচিত্রের মোট দৈর্ঘ্য। এটি বৃত্তের চারপাশে পরিমাপ করা হয়।
- ক্ষেত্রফল: বৃত্তের ক্ষেত্রফল হল বৃত্তের ভেতরের এলাকা। এটি বর্গ ইউনিটে পরিমাপ করা হয়।
বৃত্তের পরিধি এবং ক্ষেত্রফলের মধ্যে সম্পর্ক:
বৃত্তের পরিধি এবং ক্ষেত্রফলের মধ্যে একটি সম্পর্ক রয়েছে যা নিম্নলিখিত সূত্র দ্বারা প্রদান করা হয়:
C = 2πr
A = πr²
যেখানে:
- C হল বৃত্তের পরিধি
- A হল বৃত্তের ক্ষেত্রফল
- r হল বৃত্তের ব্যাসার্ধ
উদাহরণস্বরূপ:
ধরা যাক একটি বৃত্তের ব্যাসার্ধ 5 সেন্টিমিটার।
এই বৃত্তের পরিধি এবং ক্ষেত্রফল নিম্নলিখিতভাবে নির্ণয় করা যেতে পারে:
C = 2πr = 2 * 3.1416 * 5 cm = 31.42 cm A = πr² = 3.1416 * 5 cm * 5 cm = 78.54 cm²
বৃত্তের ব্যাসার্ধ নির্ণয়ের সূত্র
বৃত্তের ব্যাসার্ধ নির্ণয়ের জন্য বিভিন্ন সূত্র ব্যবহার করা যেতে পারে, নির্ভর করে আপনার কাছে কোন তথ্য উপলব্ধ তার উপর।
1. ব্যাস ব্যবহার করে:
- সূত্র: r = d/2
- যেখানে:
- r = ব্যাসার্ধ
- d = ব্যাস
উদাহরণ:
ধরা যাক একটি বৃত্তের ব্যাস 10 সেন্টিমিটার। তার ব্যাসার্ধ নির্ণয় করা যাবে:
r = d/2 = 10 cm / 2 = 5 cm
2. পরিধি ব্যবহার করে:
- সূত্র: r = C / (2π)
- যেখানে:
- r = ব্যাসার্ধ
- C = পরিধি
- π (পাই) = একটি ধ্রুবক যার মান প্রায় 3.1416
উদাহরণ:
ধরা যাক একটি বৃত্তের পরিধি 31.42 সেন্টিমিটার। তার ব্যাসার্ধ নির্ণয় করা যাবে:
r = C / (2π) = 31.42 cm / (2 * 3.1416) = 5 cm
3. ক্ষেত্রফল ব্যবহার করে:
- সূত্র: r = √(A / π)
- যেখানে:
- r = ব্যাসার্ধ
- A = ক্ষেত্রফল
- π (পাই) = একটি ধ্রুবক যার মান প্রায় 3.1416
উদাহরণ:
ধরা যাক একটি বৃত্তের ক্ষেত্রফল 78.54 বর্গ সেন্টিমিটার। তার ব্যাসার্ধ নির্ণয় করা যাবে:
r = √(A / π) = √(78.54 cm² / 3.1416) = 5 cm
আরও পড়ুন: ভাগফল নির্ণয়ের সূত্র | নিঃশেষে বিভাজ্যের ক্ষেত্রে ভাজ্য, ভাজক নির্ণয়ের সূত্র
